Introducción
Recordemos que un péndulo oscila alrededor de una posición
de equilibrio, para el caso de un péndulo con una amplitud inicial menor a π/2
el periodo T está dado por la expresión:
P.1.1Donde L es la longitud del péndulo, Ɵ es la amplitud de
oscilación medida con respecto a la vertical y g es la aceleración de la
gravedad.
Obtener el valor de g a través de esta relación seria complicado por la forma del factor entre paréntesis, por lo que sería conveniente hacer una aproximación. Si el experimento se realiza para pequeñas amplitudes, digamos para ángulos menores a 5°, el seno del ángulo sería muy pequeño por lo que todos los sumandos de la expresión que contiene este término se pueden despreciar. De esta forma el periodo del péndulo estaría dado por:
P.1.2
Con lo cual si queremos obtener g sería más simple.
Para hacer uso de esta expresión en nuestro experimento es
necesario comprobar si la condición de independencia de la amplitud se puede
cumplir.
Teóricamente se debe cumplir para ángulos menores a 5°.
Partiendo de la relación P.1.1 y llamando a 
(periodo cero teórico). Y 
La relación P.1.1 se puede expresar como: 
P.1.3
Ahora bien al realizar el experimento,
variando la amplitud, calculando con la expresión P.1.2, tomando en cuenta los
errores experimentales el periodo estará dado por:
Donde T0m es el periodo medido y ΔT es el valor absoluto de la incertidumbre.
Entonces debemos comparar ΔT0(θ)
con ΔT y si es menor entonces experimentalmente no podremos detectar las
variaciones en el periodo por la amplitud, por el contrario si es mayor
estaremos midiendo las variaciones en el periodo por la amplitud. Entonces para
saber en que rango de amplitud el periodo es independiente de esta debemos
evaluar para:
Calculando con las dimensiones de un péndulo de L=1.0m, g=10m/s2 y una incertidumbre en el periodo ΔT=± 0.01 nos da un rango de validez para θ < 48°
Ahora para calcular la validez de la
relación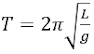 
podemos hacer lo siguiente; tomando el
logaritmo en base 10 en ambos lados de la ecuación, se tiene:
Vemos que al hacer la gráfica de los valores Log T vs Log L se obtendría una recta.
Con este experimento, mediante el análisis de un péndulo simple, obtener el valor de la aceleración de la gravedad.
Si el estudiante reacomoda el procedimiento aquí escrito con el objetivo de obtener g, tendría en ejemplo de lo que es la planeación de un experimento. Paralelamente se pretende que el estudiante revise y ejercite sus conocimientos de la teoría de errores aplicándolos al análisis e interpretación de los datos de este experimento.
Análisis de errores:
No hay comentarios:
Publicar un comentario