Planeación-Mecánica Clásica

 

 

Práctica 1. Mecánica Clásica

Análisis del péndulo simple.

I.                   Introducción

En esta práctica analizaremos las variables involucradas en la construcción y movimiento de un oscilador y como afectan estas al periodo de oscilación del oscilador. Experimentaremos con un péndulo simple y con un oscilador masa resorte.

Además no olvides que en las mediciones que realices debes considerar la incertidumbre para posteriormente calcular la incertidumbre de tus resultados

II.                Objetivo

El alumno comprobara la dependencia del movimiento de un oscilador armónico con las variables físicas involucradas en este; como la longitud, masa, amplitud de las oscilaciones, etc.

III.             Fundamentación teórica

Oscilaciones, Movimiento armónico simple, péndulo simple, oscilador masa resorte, ley de Hooke

Análisis para el experimento del péndulo

 Introducción

Recordemos que un péndulo oscila alrededor de una posición de equilibrio, para el caso de un péndulo con una amplitud inicial menor a π/2 el periodo T está dado por la expresión:

        P.1.1

Donde L es la longitud del péndulo, Ɵ es la amplitud de oscilación medida con respecto a la vertical y g es la aceleración de la gravedad.

Práctica 2. Mecánica Clásica. movimiento circular-tiro parabólico

Cuando el movimiento circular se convierte en tiro parabólico.

I.                   Objetivo

Encontrar la relación entre la velocidad tangencial de una esfera en la parte más baja de su trayectoria circular con la trayectoria parabólica que describe cuando no completa la trayectoria circular.

II.                Fundamentación teórica

Movimiento circular, conservación de la energía, movimiento oscilatorio, tiro parabólico. (preparar un resumen)

III.             Introducción

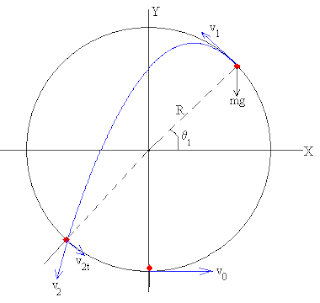
En este experimento  analizaremos  las posibles trayectorias de una esfera que cuelga de un hilo, inicialmente la esfera tomaría un movimiento circular alrededor de un punto central en donde está atado el hilo, un clavo. El problema consiste en encontrar la relación  entre la velocidad tangencial que debe tener la esfera en la parte más baja con la trayectoria parabólica, cuando no termina la trayectoria circular. Linea azul en la figura.

Figura 1. Cambio de trayectoria circular a parabólica

Práctica 3. Mecánica Clásica. Péndulo Bifilar

Practica 2. Péndulo Bifilar

I.                   Objetivo

Determinar la relación funcional del periodo de oscilación “T” del péndulo, oscilando en el plano perpendicular, en función de la longitud “L” de los hilos que lo sostienen.

II.                Fundamentación teórica

Oscilaciones armónicas, péndulo bifilar, análisis dimensional.

III.             Introducción.

Un péndulo bifilar está constituido por una barra cilíndrica homogénea suspendida en posición horizontal, por dos hilos inextensibles de igual longitud L. Los hilos sostienen la barra desde puntos equidistantes del punto medio de la barra (ver figura 1).

Práctica 4. Mecánica Clásica. Balanza de torsión

Practica 3. Balanza de torsión, El experimento de Cavendish.

Una balanza de torsión consiste en una ligera varilla con dos esferas de masa m en sus extremos, que se mantiene horizontal cuando está suspendida por su punto medio O mediante un hilo sujeto por su extremo superior P, como se muestra en perspectiva en la figura 2. Supondremos que la semilongitud de la varilla es L y que su masa es despreciable frente a las de las esferas. En estas condiciones, cuando se aparta la varilla del equilibrio manteniéndola siempre horizontal y girándola un pequeño ángulo θ , las esferas tienden a describir un movimiento  circular  con  velocidad angular ω = dθ / dt y con radio L.
Link del equipo de laboratorio, Manual técnico y de uso: https://d2n0lz049icia2.cloudfront.net/product_document/Gravitational-Torsion-Balance-Manual-AP-8215A.pdf

  a) Determine la expresión del módulo del momento angular L₀ de las dos esferas respecto al centro O de la varilla.

Al girar el sistema varilla-esferas el hilo del cual está suspendido se opone a que lo “corchen” ejerciendo un momento de torsión, τ , sobre la varilla cuyo valor es proporcional al ángulo girado θ , siempre que este ángulo sea muy pequeño. Es decir,

τ = −kθ

Práctica 5. Mecánica Clásica. Figuras de Lissajous

Superposición de MAS. Figuras de Lissajous

1. En la misma dirección

1.1. Objetivos

Analizar el fenómeno de las pulsaciones en dos MAS de frecuencias diferentes, pero muy similares, que se superponen en la misma dirección.

1.2. Material

2 generadores de señal

1 osciloscopio

2 Cables BNC-BNC

1.3. Desarrollo experimental

En primer lugar programamos dos señales de la misma amplitud en cada uno de los generadores, una de ellas a una frecuencia de 100Hz y la otra a 120Hz. Conectamos los  generadores a cada uno de los canales del osciloscopio y realizamos la superposición mediante la función de “suma” (Add). El resultado en la pantalla del osciloscopio ¿es similar al resultado teórico?, tema suma de ondas (pulsaciones).

Asimismo comprobamos que al variar la frecuencia de alguna de las dos señales variaba la amplitud de los paquetes de la señal modulada.

Péndulo Balístico

 

Práctica 3. Movimiento armónico Simple

I.                   Introducción

El estudio del movimiento armónico simple es muy importante en la Física ya que son muchos los fenómenos físicos que se relacionan con el mismo, ya sea fenómenos estudiados al analizar el comportamiento de la Naturaleza como también por el sin número de fenómenos creados por el hombre y basados en dicho movimiento.

En un movimiento armónico simple MAS, una partícula oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una función senoidal. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste, llamada fuerza recuperadora. Es un movimiento oscilatorio periódico en ausencia de fricción, donde la acción la fuerza recuperadora es directamente proporcional al desplazamiento pero en sentido opuesto.

Figura 2.1

Práctica 3. OSCILACIONES II

Objetivo

                Graficar la posición, velocidad y aceleración de un sistema con movimiento oscilatorio, asi como su energía.

Fundamentación teórica

FUERZA, POSICIÓN, VELOCIDAD, ACELERACIÓN Y ENERGIA EN EL M.A.S.

MATERIALES

·         Carrito.                                  Pesas

·         Riel.                                       Dinamómetro

·         Un resorte.

·         Hilo de 1 m de longitud.

·         Polea.

·         Mordaza de mesa.

·         Foto compuerta.

·         Regleta.

·

Figura 2.1