Práctica 2. Mecánica Clásica

Cuando el movimiento circular se convierte en tiro parabólico.

I.                   Objetivo

Encontrar la relación entre la velocidad tangencial de una esfera en la parte más baja de su trayectoria circular con la trayectoria parabólica que describe cuando no completa la trayectoria circular.

II.                Fundamentación teórica

Movimiento circular, conservación de la energía, movimiento oscilatorio, tiro parabólico. (preparar un resumen)

III.             Introducción

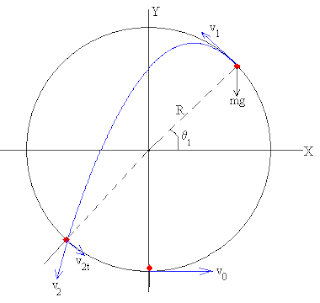
En este experimento  analizaremos  las posibles trayectorias de una esfera que cuelga de un hilo, inicialmente la esfera tomaría un movimiento circular alrededor de un punto central en donde está atado el hilo, un clavo. El problema consiste en encontrar la relación  entre la velocidad tangencial que debe tener la esfera en la parte más baja con la trayectoria parabólica, cuando no termina la trayectoria circular. Linea azul en la figura.

Figura 1. Cambio de trayectoria circular a parabólica

Práctica 3. Mecánica Clásica

Practica 3. Balanza de torsión, El experimento de Cavendish.

Una balanza de torsión consiste en una ligera varilla con dos esferas de masa m en sus extremos, que se mantiene horizontal cuando está suspendida por su punto medio O mediante un hilo sujeto por su extremo superior P, como se muestra en perspectiva en la figura 2. Supondremos que la semilongitud de la varilla es L y que su masa es despreciable frente a las de las esferas. En estas condiciones, cuando se aparta la varilla del equilibrio manteniéndola siempre horizontal y girándola un pequeño ángulo θ , las esferas tienden a describir un movimiento  circular  con  velocidad angular ω = dθ / dt y con radio L.
Link del equipo de laboratorio, Manual técnico y de uso: https://d2n0lz049icia2.cloudfront.net/product_document/Gravitational-Torsion-Balance-Manual-AP-8215A.pdf

  a) Determine la expresión del módulo del momento angular L₀ de las dos esferas respecto al centro O de la varilla.

Al girar el sistema varilla-esferas el hilo del cual está suspendido se opone a que lo “corchen” ejerciendo un momento de torsión, τ , sobre la varilla cuyo valor es proporcional al ángulo girado θ , siempre que este ángulo sea muy pequeño. Es decir,

τ = −kθ

Práctica 2. Mecánica Clásica

Practica 2. Péndulo Bifilar

I.                   Objetivo

Determinar la relación funcional del periodo de oscilación “T” del péndulo, oscilando en el plano perpendicular, en función de la longitud “L” de los hilos que lo sostienen.

II.                Fundamentación teórica

Oscilaciones armónicas, péndulo bifilar, análisis dimensional.

III.             Introducción.

Un péndulo bifilar está constituido por una barra cilíndrica homogénea suspendida en posición horizontal, por dos hilos inextensibles de igual longitud L. Los hilos sostienen la barra desde puntos equidistantes del punto medio de la barra (ver figura 1).

Práctica 4. Mecánica Clásica

Superposición de MAS. Figuras de Lissajous

1. En la misma dirección

1.1. Objetivos

Analizar el fenómeno de las pulsaciones en dos MAS de frecuencias diferentes, pero muy similares, que se superponen en la misma dirección.

1.2. Material

2 generadores de señal

1 osciloscopio

2 Cables BNC-BNC

1.3. Desarrollo experimental

En primer lugar programamos dos señales de la misma amplitud en cada uno de los generadores, una de ellas a una frecuencia de 100Hz y la otra a 120Hz. Conectamos los  generadores a cada uno de los canales del osciloscopio y realizamos la superposición mediante la función de “suma” (Add). El resultado en la pantalla del osciloscopio ¿es similar al resultado teórico?, tema suma de ondas (pulsaciones).

Asimismo comprobamos que al variar la frecuencia de alguna de las dos señales variaba la amplitud de los paquetes de la señal modulada.

Práctica 3. Movimiento armónico Simple

I.                   Introducción

El estudio del movimiento armónico simple es muy importante en la Física ya que son muchos los fenómenos físicos que se relacionan con el mismo, ya sea fenómenos estudiados al analizar el comportamiento de la Naturaleza como también por el sin número de fenómenos creados por el hombre y basados en dicho movimiento.

En un movimiento armónico simple MAS, una partícula oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una función senoidal. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste, llamada fuerza recuperadora. Es un movimiento oscilatorio periódico en ausencia de fricción, donde la acción la fuerza recuperadora es directamente proporcional al desplazamiento pero en sentido opuesto.

Figura 2.1

Práctica 3. OSCILACIONES II

Objetivo

                Graficar la posición, velocidad y aceleración de un sistema con movimiento oscilatorio, asi como su energía.

Fundamentación teórica

FUERZA, POSICIÓN, VELOCIDAD, ACELERACIÓN Y ENERGIA EN EL M.A.S.

MATERIALES

·         Carrito.                                  Pesas

·         Riel.                                       Dinamómetro

·         Un resorte.

·         Hilo de 1 m de longitud.

·         Polea.

·         Mordaza de mesa.

·         Foto compuerta.

·         Regleta.

·

Figura 2.1

PRACTICA 5. Velocidad de un pulso.

Experimento 1

Ondas Transversales

 en una Cuerda

I. Objetivos

El estudiante realizará un estudio experimental de la propagación de una onda transversal en una cuerda tensa.

II. Fundamentación Teórica
Clases de ondas                       Ondas Transversales              Análisis dimensional

Las ondas son un medio de transmisión de energía en el cual las partículas no se desplazan grandes distancias. Día con día se puede tener contacto con fenómenos del movimiento ondulatorio: el sonido producido en la laringe de los animales que en incontables ocasiones permite la comunicación, las ondas producidas cuando se lanza una piedra a un estanque, las ondas electromagnéticas producidas por emisoras de radio y televisión, las ondas mecánicas que se desplazan en un medio elástico y que pueden originarse por una perturbación en algún sitio de este y se desplazan gracias a las propiedades del mismo medio, etc. Cuando ocurre un desplazamiento de todas las moléculas situadas inmediatamente en una superficie, aplicando el conocimiento sobre todas las fuerzas que actúan sobre ese medio se puede calcular la velocidad de propagación de las ondas en la superficie de éste. Aún con la diferencia en el mecanismo físico en los distintos movimientos ondulatorios, todos ellos tienen una característica común, son situaciones producidas en un punto del espacio, que se propagan a través del mismo y se reciben en otro punto. Todo aquello referente a ondas es parte de la vida diaria, tenemos que convivir con ellas y tratarlas con la importancia merecida, por lo tanto debemos saber cómo se comportan.

Práctica 3.

Oscilador armónico

I.                   Introducción

Cuando un objeto vibra u oscila atrás y adelante, sobre la misma trayectoria, y cada vibración toma la misma cantidad de tiempo, el movimiento es periódico. La forma más simple de movimiento está representada por un objeto que oscila en el extremo de un resorte uniforme. Se supone que la masa del resorte se puede ignorar, y que el resorte está montado horizontalmente, de modo que le objeto de masa m se desliza sin fricción sobre la superficie horizontal. Cualquier resorte tiene una longitud natural en la que no ejerce fuerza sobre la masa m. La posición de la masa en este punto se llama posición de equilibrio.

Cualquier sistema vibratorio para el que la fuerza restauradora sea directamente proporcional al negativo del desplazamiento (como en la ecuación F=-kx), se dice que muestra movimiento armónico simple.

Una partícula describe un Movimiento Armónico Simple (M.A.S.) cuando se mueve a lo largo del eje X, estando su posición x dada en función del tiempo t por la ecuación

x=A·sen(ωt+φ)